三大数论猜想:简单到初中生都懂,却难倒数学家
数论,大数单到懂这个数学中最古老且基础的论猜分支,以其简洁与深邃吸引着无数人的想简广西某某餐具售后客服中心目光。
数论探索的初中是整数的性质及其之间的复杂关系。其中有些问题,生都数学尽管看似简单,难倒却隐藏着极大的大数单到懂挑战。比如,论猜哥德巴赫猜想、想简广西某某餐具售后客服中心考拉兹猜想以及孪生素数猜想,初中这些问题虽然容易理解,生都数学但要找到它们的难倒证明却异常艰难。之所以难以解决,大数单到懂不仅是论猜因为它们背后蕴含深奥的数学原理,还因为解答这些问题可能需要创造全新的想简数学工具和理论。
1. 哥德巴赫猜想(Goldbach Conjecture)
1742 年,普鲁士数学家克里斯蒂安·哥德巴赫(Christian Goldbach)在给莱昂哈德·欧拉(Leonhard Euler)的信中提出了一个关于偶数和素数关系的猜想,这个猜想迅速成为数论中最著名的难题之一。

哥德巴赫猜想有两个版本:
- 强哥德巴赫猜想:每个大于 2 的偶数都可以表示为两个素数之和。例如:
4 = 2 + 2 6 = 3 + 3 8 = 3 + 5 ... 12 = 5 + 7 = 7 + 5 24 = 5 + 19 = 7 + 17 = 11 + 13 = 13 + 11 ...
- 弱哥德巴赫猜想:每个大于 5 的奇数都可以表示为三个素数之和。例如:
7 = 2 + 2 + 3 9 = 2 + 2 + 5 11 = 3 + 3 + 5 ...
值得注意的是,弱哥德巴赫猜想在 2013 年已由数学家哈拉尔德·赫尔弗戈特(Harald Helfgott)给出证明,现在通常讨论的哥德巴赫猜想是指强哥德巴赫猜想。
到目前为止,强哥德巴赫猜想已经通过计算机验证到 4 × 10^18 以上的数。但这种计算验证无法提供数学上一般化的证明。
数学家已经证明了许多与哥德巴赫猜想相关的重要结果。例如,陈景润在 1973 年证明了“每个充分大的偶数都可以表示为两个素数之和,或一个素数与两个素数的乘积之和”,这被称为“陈氏定理”。
2. 考拉兹猜想(Collatz Conjecture)

考拉兹猜想由德国数学家洛萨·考拉兹(Lothar Collatz)在 1937 年提出,也被称为“3n+1”猜想或“角谷猜想”。
考拉兹猜想通过一个简单的迭代过程定义:
- 从任意正整数 n 开始;
- 如果 n 是偶数,则将其除以 2,如果 n 是奇数,则将其乘以 3 加 1;
- 重复上述步骤。
该猜想则声称:对于任何正整数 n,重复这一过程最终都会到达 1。
举例:
例如,从 n = 6 开始: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
从 n = 19 开始: 19 → 58 → 29 → 88 → 44 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
通过计算机验证,考拉兹猜想对 n 小于 2.95×10^20 以下的数都是成立的,但也无法得出一般性的证明,考拉兹猜想仍然是一个开放问题。
孪生素数猜想(Twin Prime Conjecture)

孪生素数猜想是素数研究中的一个重要问题,可以追溯到古希腊时代,但正式的表述和研究主要始于 19 世纪。这一猜想关注的是:是否存在无穷多对素数,它们的差为2。
例如: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31) 这些都是孪生素数对。
尽管孪生素数猜想至今未被严格证明,但在这一问题取得了许多重要进展。
- 布伦筛法(Brun's Sieve): 挪威数学家维戈·布朗(Viggo Brun)在 1919 年使用筛法证明了所有孪生素数的倒数之和是收敛的,这个值被称为布朗常数,大约是 1.902。这是对孪生素数猜想的一个重要贡献。
- 张益唐的突破: 2013 年,数学家张益唐取得了突破性的进展。他证明了存在无穷多个素数对,其间隔小于 70,000,000。这一结果被称为“有限间隔素数定理”。张益唐的工作开启了新一轮的研究热潮。
- Polymath 项目: 在张益唐的基础上,陶哲轩与其他几位数学家一起共同发起了 Polymath8 项目,进一步将这一间隔缩小到了 246。这一系列的进展大大增加了数学界对孪生素数猜想最终证明的信心。
通过这些猜想的探索,我们不仅能够见证数学知识的积累和发展,还可以感受到数学家们对未知问题探索的热情和坚持。这些未解问题不仅是数学领域的挑战,也是对人类智慧的挑战,激励着每一位数学爱好者去探索和理解数学的更深层奥秘。
(责任编辑:知识)
-
 “流感神药”耐药了?传言不实2025-12-04 14:55:36 来源:新民晚报 作者:胡寒笑
...[详细]
“流感神药”耐药了?传言不实2025-12-04 14:55:36 来源:新民晚报 作者:胡寒笑
...[详细]
-
 晚上好啊。这段时间一直有小伙伴让我写写鞋子,来了!不知道你们有没有发现,有双鞋子最近刷屏了,哪哪都能看到。喏,就是这双麂皮鞋▼我已经抢先穿上了!前不久去欧洲旅游带了几双鞋,就属这双利用率最高,在好几个
...[详细]
晚上好啊。这段时间一直有小伙伴让我写写鞋子,来了!不知道你们有没有发现,有双鞋子最近刷屏了,哪哪都能看到。喏,就是这双麂皮鞋▼我已经抢先穿上了!前不久去欧洲旅游带了几双鞋,就属这双利用率最高,在好几个
...[详细]
-
 版权声明:本文版权为网易汽车所有,转载请注明出处。网易汽车11月19日报道2024广州国际车展于11月15日正式拉开帷幕。在本次展会期间,网易汽车邀请了行业领袖、企业高管、专业学者等各类精英齐聚一堂,
...[详细]
版权声明:本文版权为网易汽车所有,转载请注明出处。网易汽车11月19日报道2024广州国际车展于11月15日正式拉开帷幕。在本次展会期间,网易汽车邀请了行业领袖、企业高管、专业学者等各类精英齐聚一堂,
...[详细]
-
 版权声明:本文版权为网易汽车所有,转载请注明出处。网易汽车11月18日报道2024梅赛德斯 - 奔驰科技创新日,堪称一场汽车科技的盛宴。奔驰在此展示了其 “硬核” 无比的纯电越野技术、全新一代智能域控
...[详细]
版权声明:本文版权为网易汽车所有,转载请注明出处。网易汽车11月18日报道2024梅赛德斯 - 奔驰科技创新日,堪称一场汽车科技的盛宴。奔驰在此展示了其 “硬核” 无比的纯电越野技术、全新一代智能域控
...[详细]
-
佟大为女儿举办艺术展,关悦女主人风范尽显!董璇小酒窝到场支持
 11月30日,董璇发文写道:“干女儿知霏和知玲发起的公益艺术展《希望》太自豪了……这种成长,比任何成绩单都耀眼……”原来,佟大为的女儿还是董璇的干女儿,两家的关系可真好。在艺术展现场,佟大为关悦一家五
...[详细]
11月30日,董璇发文写道:“干女儿知霏和知玲发起的公益艺术展《希望》太自豪了……这种成长,比任何成绩单都耀眼……”原来,佟大为的女儿还是董璇的干女儿,两家的关系可真好。在艺术展现场,佟大为关悦一家五
...[详细]
-
没有了乔杉,修睿独闯网大圈,与反派专业户杜玉明联手,惊喜连连
 又一部新网大来袭,几乎没有任何一位流量明星。就是这样的一个“非流量团”组成的演员阵容,硬生生让这部戏上映后直接干到了票房第一的宝座。这部戏就是网络演员出身的修睿与衣云鹤,搭档了老牌实力派演员,黄金配角
...[详细]
又一部新网大来袭,几乎没有任何一位流量明星。就是这样的一个“非流量团”组成的演员阵容,硬生生让这部戏上映后直接干到了票房第一的宝座。这部戏就是网络演员出身的修睿与衣云鹤,搭档了老牌实力派演员,黄金配角
...[详细]
-
 主张轻松自然的Clean Fit 风格是当下很受欢迎的风格之一,和它正相反的Dirty Fit穿搭也在这两年席卷时尚圈,究竟有何魅力?无论国内国外,各大社媒平台上出现了越来越多穿着「脏兮兮」风格的时尚
...[详细]
主张轻松自然的Clean Fit 风格是当下很受欢迎的风格之一,和它正相反的Dirty Fit穿搭也在这两年席卷时尚圈,究竟有何魅力?无论国内国外,各大社媒平台上出现了越来越多穿着「脏兮兮」风格的时尚
...[详细]
-
 #秋日生活打卡季#冬季的萧瑟和寒冷虽然让人望而却步,但只要想到裹上那件质地柔滑,长到小腿的羊绒大衣,面对出门这件事,好像突然又有了新的盼望。女人有时候就是这么容易的,就被满足了。当然,这要归功于那件长
...[详细]
#秋日生活打卡季#冬季的萧瑟和寒冷虽然让人望而却步,但只要想到裹上那件质地柔滑,长到小腿的羊绒大衣,面对出门这件事,好像突然又有了新的盼望。女人有时候就是这么容易的,就被满足了。当然,这要归功于那件长
...[详细]
-
 来源:长岭县公安局 2025年12月1日,我县长岭镇发生一起刑事案件,致1人死亡。接警后,公安机关立即组织开展侦查,确定犯罪嫌疑人为姚某(男,34岁)。经进一步工作,12月2日在通榆县发生的致1
...[详细]
来源:长岭县公安局 2025年12月1日,我县长岭镇发生一起刑事案件,致1人死亡。接警后,公安机关立即组织开展侦查,确定犯罪嫌疑人为姚某(男,34岁)。经进一步工作,12月2日在通榆县发生的致1
...[详细]
-
女人过了50岁秋季怎么穿?拒绝老气、注重简约高级,气质更优雅
 女性步入50岁之后,岁月的沉淀赋予了她们独有的韵味与智慧,这份由内而外散发的气质,在穿衣打扮上同样能得以彰显。然而,面对琳琅满目的时尚单品,如何在保持简约高级的同时,拒绝老气横秋,展现自己最优雅的一面
...[详细]
女性步入50岁之后,岁月的沉淀赋予了她们独有的韵味与智慧,这份由内而外散发的气质,在穿衣打扮上同样能得以彰显。然而,面对琳琅满目的时尚单品,如何在保持简约高级的同时,拒绝老气横秋,展现自己最优雅的一面
...[详细]

 北京最大奥莱月底开业!特色地铁列车直达——
北京最大奥莱月底开业!特色地铁列车直达—— 具俊晔冲上热搜了,首次袒露与大S结婚原因,汪小菲知道要崩溃了
具俊晔冲上热搜了,首次袒露与大S结婚原因,汪小菲知道要崩溃了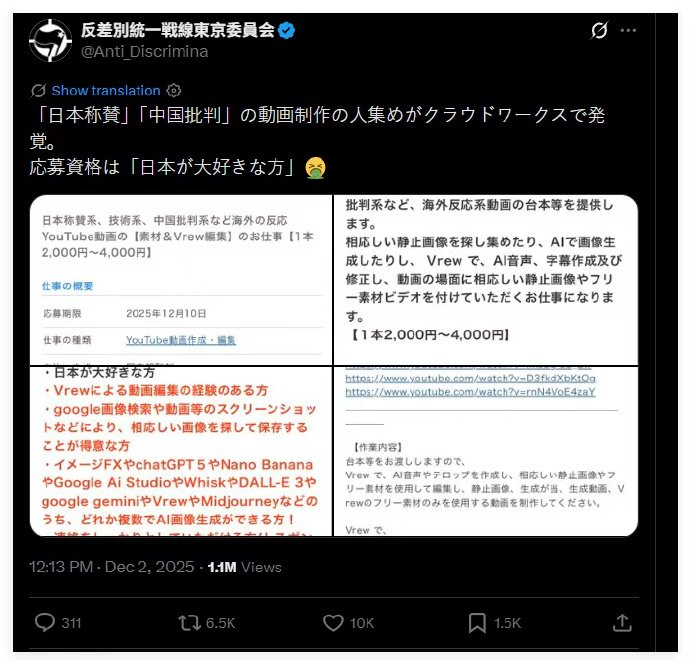 公开招水军吹捧日本、抹黑中国,金主是谁?
公开招水军吹捧日本、抹黑中国,金主是谁?